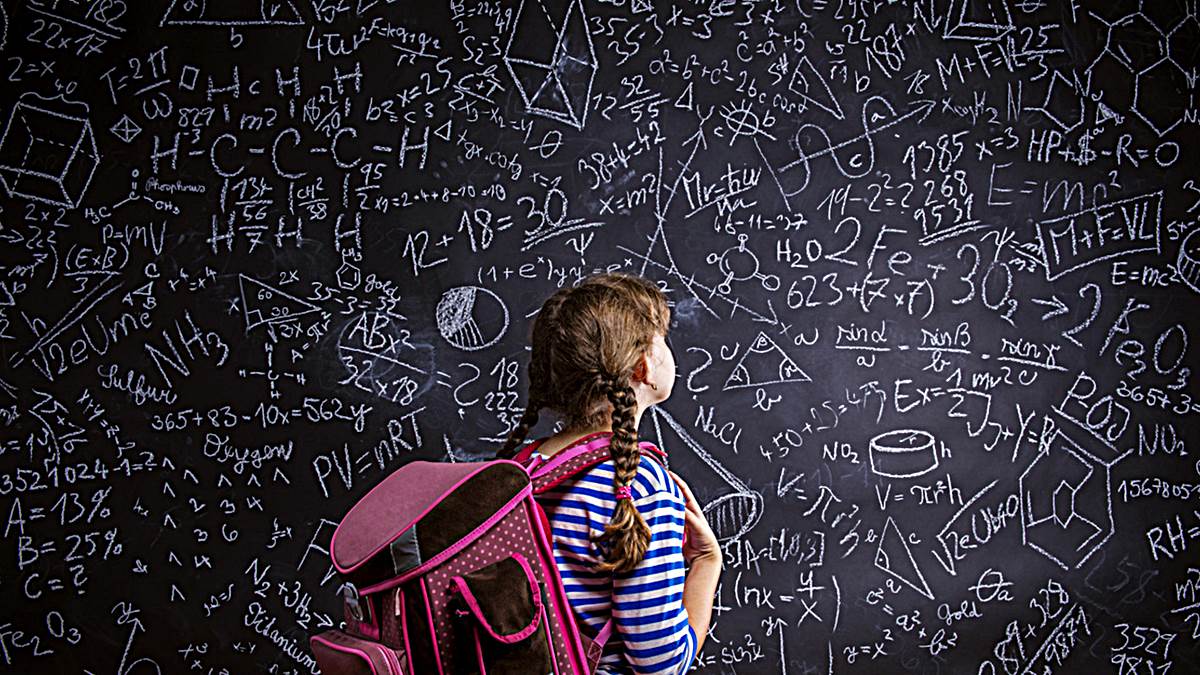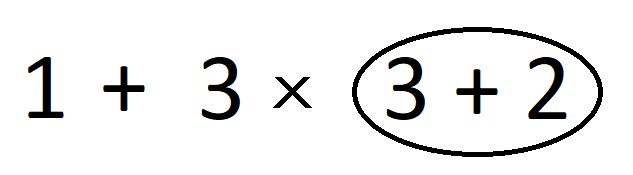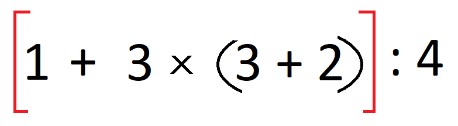¿Dudas del currículo?
Yo siempre he pensado (y dicho) que lo primero que tenemos que hacer los profes es dudar del currículo. El currículo nos dice qué hacer y cuándo hacerlo y ahí es donde se le ven las costuras a la ley educativa (sea cual sea). Ahí es cuando se ve que no se ha tenido en cuenta cómo y cuándo aprenden los niños.
El “cómo” viene determinado por los procesos que sigue la cabecita del niño en función de su edad y desarrollo madurativo. Es decir, si se sabe que el cerebro ha de seguir unas fases para poder dar por aprendido y asentado un conocimiento, ¿por qué no se respeta? ¿Por qué no se contempla el aprendizaje “procesual” en las leyes educativas?
El “cuándo” viene determinado por el momento en que se enfrenta el niño a un nuevo aprendizaje (en función de lo que ha ido construyendo y del desarrollo anterior). Claro, no todos los niños van al mismo ritmo. Y, además, no es lo mismo un niño de enero que uno de diciembre, pero… ¿Qué menos que el orden de los contenidos a aprender tenga un poquito de lógica y secuencia adecuada? Mirad, unos ejemplitos rápidos para que sepáis de que hablo:
- Los niños acaban infantil con los números hasta el nueve.
- Los niños acaban infantil con la lectura de las horas en punto en un reloj analógico (el de las agujas).
¡Espera, espera! ¡Las horas del reloj son 12! ¿Da igual haber trabajado solo hasta el 9?
Seguimos con el reloj. En primero de primaria nos piden que el niño lea el reloj (“en punto” e “y media”). En segundo nos piden, además, “y cuarto” y “menos cuarto”.
¿En serio que no pensaron que “quizá” era buena idea que el niño sepa qué es “medio”, qué es “cuarto” y qué es “3 cuartos” para poder comprender el reloj? No digo que hagan un estudio profundo de fracciones (que están contempladas en 3.ºEP o 4.ºEP (según autonomía)) pero, hombre, pedirles que hagan un acto de fe en cuanto al reloj se refiere cuando se puede dotar de comprensión parece un poco desafortunado, ¿no?
Bueno, a lo que vamos en esta entrada: la jerarquía de las operaciones.
Pero…¿¿¡¡Cómo va a estar este contenido en 5.ºEP y 6.ºEP si se trabaja y construye desde infantil!!??
Juegos desde que son muy pequeños para preparar la jerarquía de las operaciones.
Imaginad que estamos trabajando clasificaciones en infantil. ¿Qué tendrá eso que ver con la futura jerarquía?
Niños, tenemos un reto. En cada uno de los 3 recipientes tenéis que meter 2 triángulos azules y 3 círculos rojos.
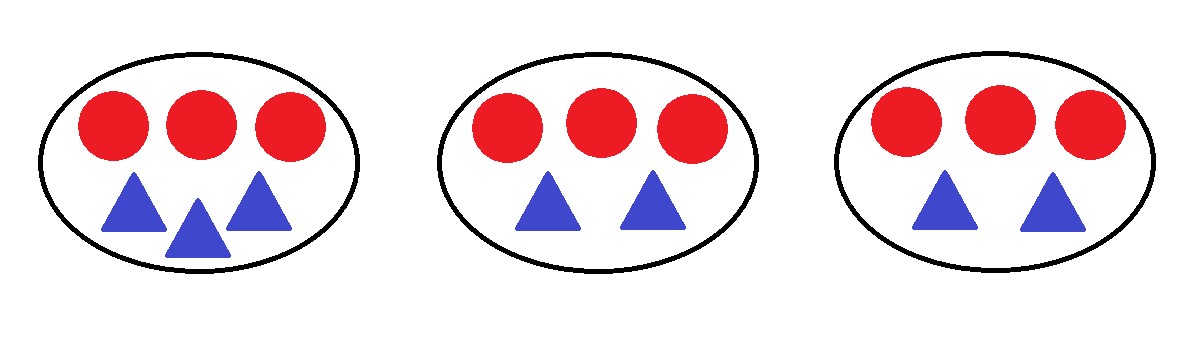
Después de dejar que discriminen por color y forma un rato, acaban por tener algo así:
¿Qué has metido aquí? (señalando el primer conjunto). 3 círculos rojos y 2 triángulos azules.
¿Y aquí? (señalando segundo conjunto). 3 círculos rojos y 2 triángulos azules.
¿Y aquí? (señalando tercer conjunto). 3 círculos rojos y 2 triángulos azules.
Y aquí paramos por el momento. No hace falta más. No se pretende más. Solo estamos sembrando semillitas.
Más adelante repetiremos actividades de este tipo y añadiremos algunas preguntas:
- ¿Qué hay en cada recipiente?
- ¿Cuántos recipientes hay?
- ¿Cuántas piezas hay en cada recipiente?
- ¿Cuántas en este? 5. ¿Y en este? 5. ¿Y este? 5.
Y aquí paramos por el momento. No se pretende más. Solo estamos preparando el terreno para para expresar con símbolos una historia. Es un “¿de qué va esto?” Va de que hay 3 recipientes y en cada uno hay 2 triángulos y 3 círculos. Va de que hay 3 recipientes y en cada uno hay 5 figuras.
Y ahora algo súper, súper, súper importante. ¿Sabes cómo se lee eso que has escrito en matemático?
¡ATENCIÓN! ACHTUNG! No se lee “tres más dos”. Se lee “en un recipiente hay 3 círculos rojos y 2 triángulos azules”.
Como ya habréis imaginado, el hecho de que el “3+2” esté metido en un óvalo no es casual. El óvalo trata de indicar que estamos hablando de un conjunto. Un conjunto de 3 elementos y 2 elementos. Esto es absolutamente determinante para poder comprender el uso de los paréntesis y para poder comprender por qué se resuelven en uno u otro orden.
¿Qué preguntar para seguir avanzando con la historia de los triángulos y los círculos que están metidos en recipientes?
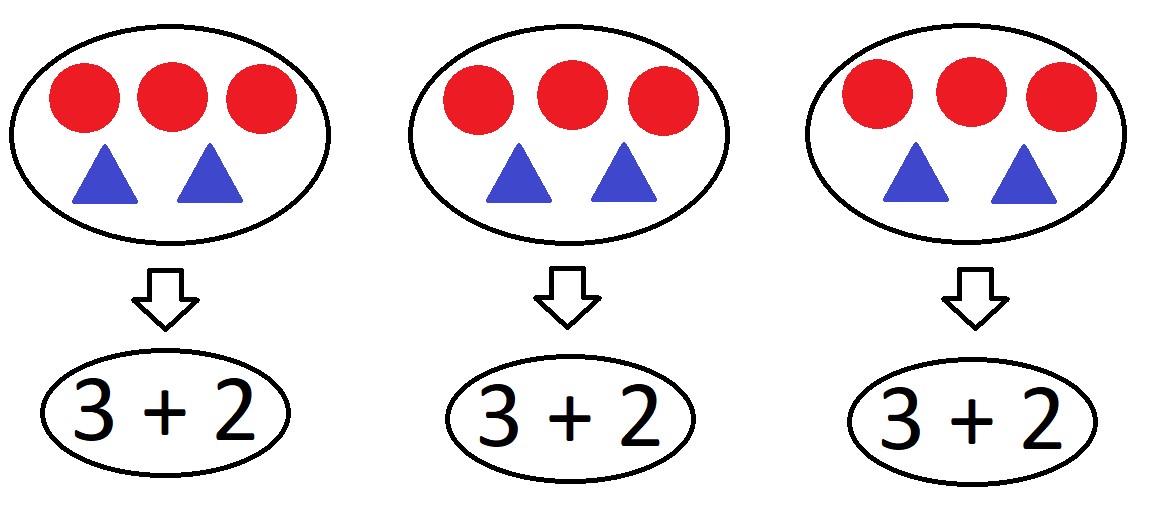
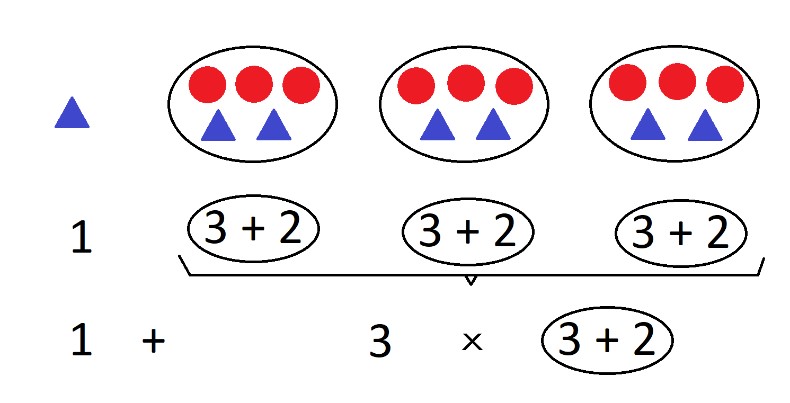
Entonces decís que en cada recipiente hay 3 círculos rojos y 2 triángulos azules y que eso se escribe “en matemático” así: “3 + 2”
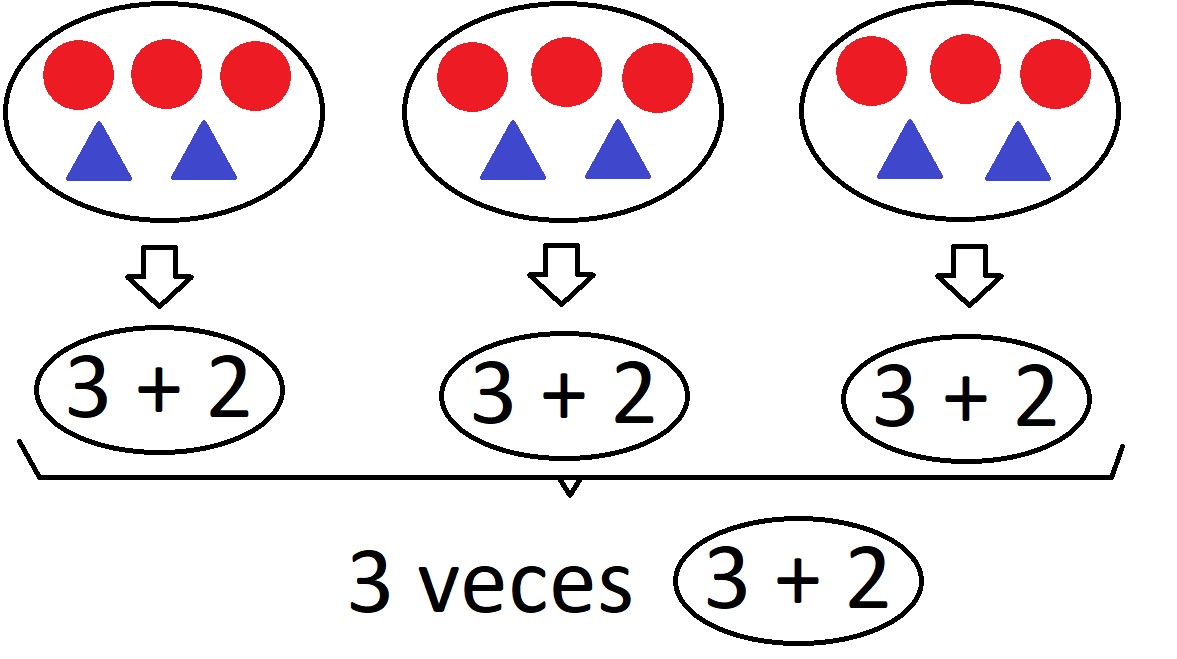
Entonces, ¿cuántas veces “3 + 2”? ¿Cuántos grupos de “3 + 2”? Tres, tres veces “3 + 2”, tres grupos de “3 + 2” ¿A ver? Vamos a escribir eso que acabáis de decir
El paso de “veces” o “grupos iguales” al símbolo “×” es inmediato. En poco tiempo tienes a los niños expresando la situación anterior como:
La historia anterior es fundamental para que el niño sepa que la acción “×” se ejecuta 3 veces sobre el conjunto “3 + 2”.
No te preocupes de momento porque el niño dibuje un óvalo en vez de unos buenos paréntesis. Ahora veremos por qué lo mantenemos de momento.
¿En qué orden opero?
Si es que da igual cómo operes. A ver, da igual si sabes qué quiere decir cada símbolo. Mirad, vamos a complicar un poquito más la situación anterior para que veamos que si verbalizamos la historia no me cabe duda de en qué orden operar.
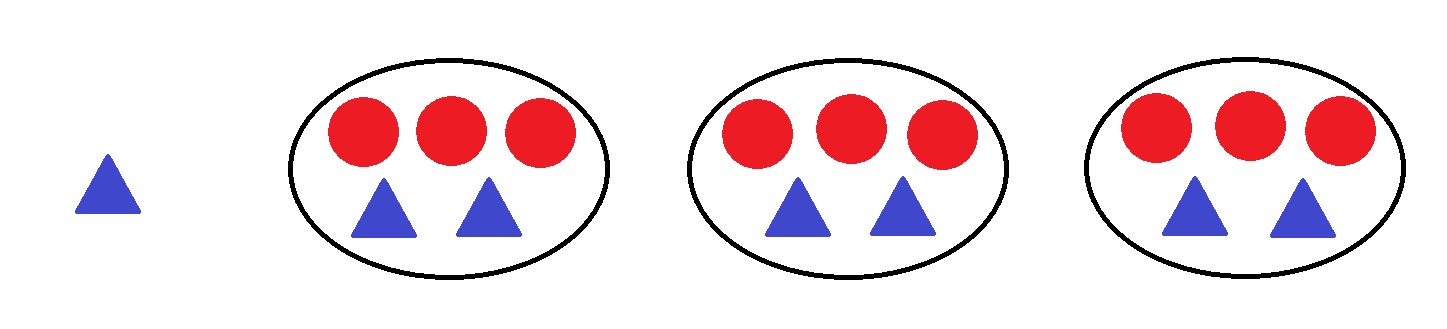
Imaginad que la situación hubiera sido esta:
Y les digo a los niños: “¿Sabéis escribir eso en matemático?” Harían algo así:
Total, que la historia dice así:
“Tengo un triángulo por ahí suelto y, además, tengo 3 recipientes y, en cada uno, hay 3 círculos y 2 triángulos”
Y la historia se escribe así:
¿Y sabéis qué? Que no hay absolutamente ningún peligro de que los niños sumen el 1 con el 3 en primer lugar,¿sabéis por qué? Porque al contar la historia vimos que el “1” juega un papel muy diferente en la historia. El 1 es un “además”. La historia principal transcurre entre los 3 recipientes con “3+2”. Como sabemos que el “3 ×” indica el número de grupos, ¿qué sentido tendría sumar el 1?
A partir de este momento, cuando sabemos que el óvalo indica un conjunto sobre el que se ejecuta la acción, podemos borrar la parte de arriba y la parte de abajo del óvalo para que quede el paréntesis. Y queda algo así:
1 + 3 × (3 + 2)
Si domino el contexto puedo jugar con los números como quiera
Bueno, bueno… Es mucho decir que no hay peligro en que el niño sume el “1” con el 3. (ironía… No hay peligro, de verdad)
Si primero manipulan y luego interpretan lo manipulado pueden crear sus propias operaciones combinadas. Imaginad que llega uno y dice: “¡Pues a mí eso de que ese triángulo esté ahí fuera no me convence! ¡Quiero meterlo en un conjunto! Y entonces pasa esto:
Y claro, la historia cambia.
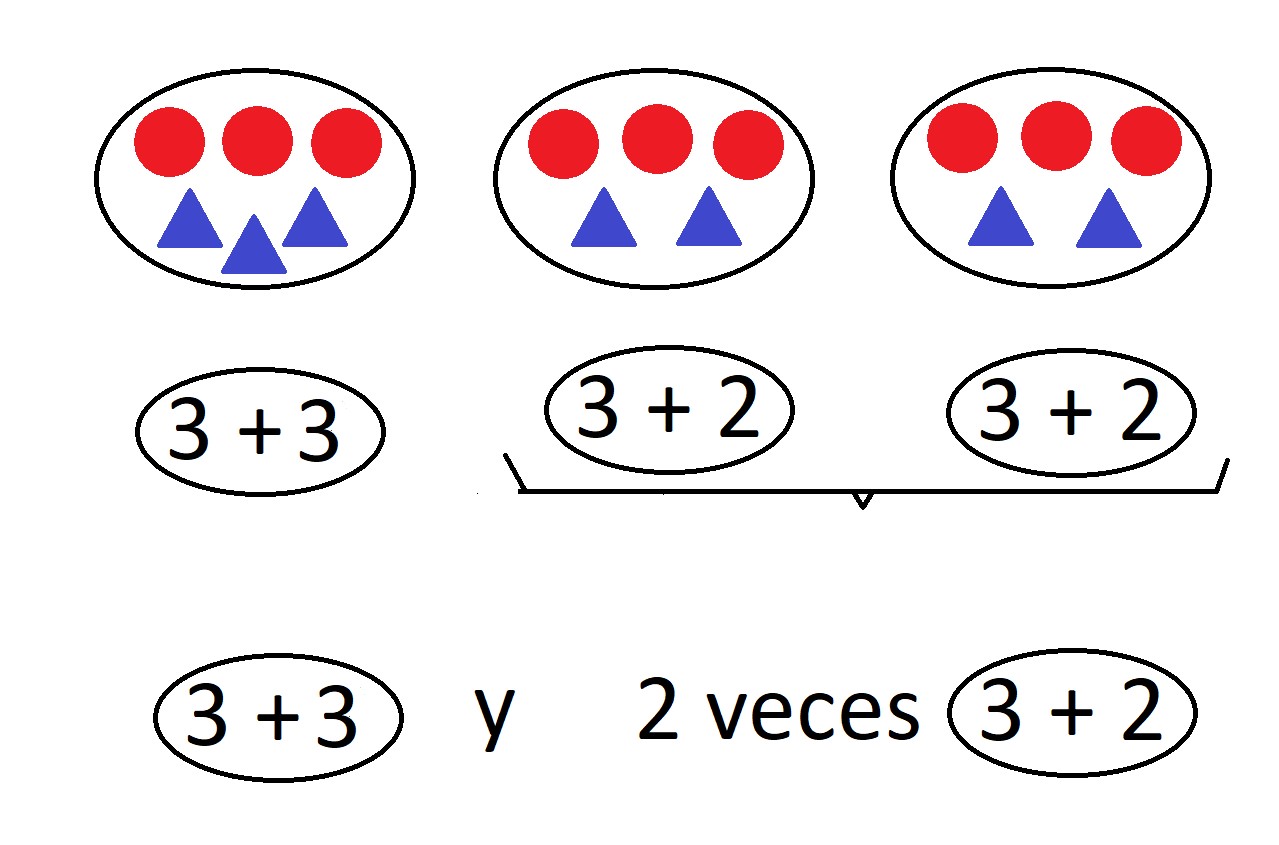
¿Me cuentas la historia? Tengo 3 recipientes. En uno tengo tres círculos y tres triángulos y en los otros tengo tres círculos y dos triángulos en cada uno. ¿Sabes escribir la historia “en matemático”? Y, entonces, después de seguir el proceso descrito antes, llegan a esto SIN PROBLEMAS:
Y, sin mayor dificultad escriben esto en matemático así:
(3 + 3) + 2 x (3 + 2)
Y, sí, es cierto que se produce un abuso de paréntesis ya que el “3 + 3” no es necesario “entreparentesisarlo”…¡Pues no haber metido el triangulito ahí dentro!
La importancia de saber “qué es todo”
Volvamos a la situación esta:
Imaginad que la historia continúa de esta manera:
Chicos, tenemos que repartir el total de piezas entre estos 4 niños. Da igual qué piezas le toquen a cada niño pero queremos que los 4 tengan la misma cantidad. ¿Cómo escribís “en matemático” esta nueva historia?
Y entonces necesitamos nuevamente preguntas intermedias que les permitan actuar sobre la expresión matemática comprendiendo en todo momento lo que hacen:
-
¿Qué tenemos que repartir? Todas las piezas.
-
¿Qué expresión matemática representa “todas las piezas”? 1 + 3 × (3 + 2)
-
Indica con un dibujo “todas las piezas”. Rodea “todas las piezas” para que sepamos el conjunto sobre el que ejecutamos la acción del reparto:
Y, después, es tan sencillo como borrar los bordes de arriba del rectángulo y del óvalo y quede esto:
Que se lee: “Hay un triángulo y, además, hay 3 recipientes que tienen 3 círculos y 2 triángulos cada uno.Todo eso lo queremos repartir entre 4 amigos”.
Hecho esto, dicho esto, NO existe dificultad en operar, en saber en qué orden se hacen. Pero claro, para que eso ocurra es necesario saber qué quiere decir cada número, qué acción representa cada símbolo.
Las operaciones SIN CONTEXTO NO ESTÁN EN LA VIDA. En la vida sé que si tengo que pagar el pantalón y la camiseta y quiero saber qué me devolverán al pagar con 50 € no me cabe duda de que resto “pantalón + camiseta” a 50 euros y no necesito saber el orden en qué resolver, ni la regla de los signos ni nada parecido. Solo necesito saber de qué va la historia para deducir qué hacer primero y qué hacer después.
¿Os acordáis de aquel reto?
A principio de curso se hizo viral una operación combinada. ¡Genial que se viralicen las mates! (porque se hace viral cada cosita…).
Bueno, el reto en cuestión fue este:
Y la duda era si el resultado debía de ser 1 o 16. ¿Qué historia se esconde detrás de esa expresión? Quizá si se dota de significado a los símbolos… Quizá si hubiera un problema, una situación en contexto podríamos haber visto si la expresión estaba correctamente escrita o no.
Pero, ¿sabéis qué? Que solo se trataba de números, que solo se trataba si debíamos seguir las reglas de resolución PEMDAS o BODMAS.
Los números son solo números y los cálculos son solo cálculos, ¡por muy abiertos que sean los cálculos! Si los números, si las operaciones no cuentan una historia no son significativas y si no son significativas entonces contravenimos lo que nos pide la ley, cualquiera de las que ha habido y de las que habrá: que el aprendizaje sea singnificativo. Y en ese anhelo de la significatividad del aprendizaje no creo que se equivoque la Ley.
Y termino esta entrada igual que la anterior:
“Lo importante no es contar sino lo que realmente cuenta”. Y me permito la licencia de añadir algo a la cita de Talbert:
LO IMPORTANTE NO ES CONTAR NÚMEROS SINO LO QUE NOS CUENTAN LOS NÚMEROS.
Para leer el articulo original pincha aquí
Profe Bernabeu