A las cosas por su nombre también cuando nos metemos de lleno en operaciones con decimales. si llamamos a las cosas por su nombre evitaremos dificultades típicas. Llamar a las cosas por su nombre se conoce en matemáticas como tener adquirido el «sentido numérico». El sentido numérico implica conocer y dominar «por dentro» los números para poder adecuarlos como me interese en función de lo que me interese.
Errores que evitamos gracias al dominio del sentido numérico
Decíamos en el artículo anterior que es frecuente que muchos niños digan que 0,7 + 0,8 es 0,15. Esto no ocurriría si nombrásemos los sumandos por su nombre: 7 décimas y 8 décimas son 15 décimas que es 1 unidad y 5 décimas.
Esto ocurre con todo. Por ejemplo con la famosa «unidad seguida de ceros». Es frecuente que le digamos a los niños, simplemente, que muevan la coma a la derecha o a la izquierda según tengan que multiplicar o dividir por la unidad seguida de ceros. No digo que no sea más rápido (claro que sí) pero… ¿Y si aseguramos primero que comprenden qué le ocurre al número y, después, vamos a la mecánica?
Imaginad esta operación:
Es típico que digamos cosas como: «busca la coma, mira a ver si tienes que multiplicar o dividir. Si tienes que multiplicar mueve la coma a la derecha tantos lugares como ceros tenga la unidad». Y entonces hacen algo así:
Eso es mecánica. No digo que esté mal. Simplemente digo que si somos coherentes con todo lo anterior, con el lenguaje, en lugar de ir a mover la coma sin más diríamos algo como: 4 décimas por cien son 400 décimas que son 40 unidades.
¿Y al dividir? Pues igual. Si tienes que dividir 4 : 100 realmente no haces otra cosa que dividir 4 unidades en 100 partes. O lo que es lo mismo, 400 centésimas en 100 partes que da como resultado 4 centésimas, que son 0 unidades, 0 décimas y 4 centésimas.
¿Que es más sencillo moviendo la coma y ya está? No es más sencillo, es más mecánico y cuando algo está comprendido pues no está mal recurrir a la mecánica, pero lo suyo es que esté comprendido antes, ¿no?
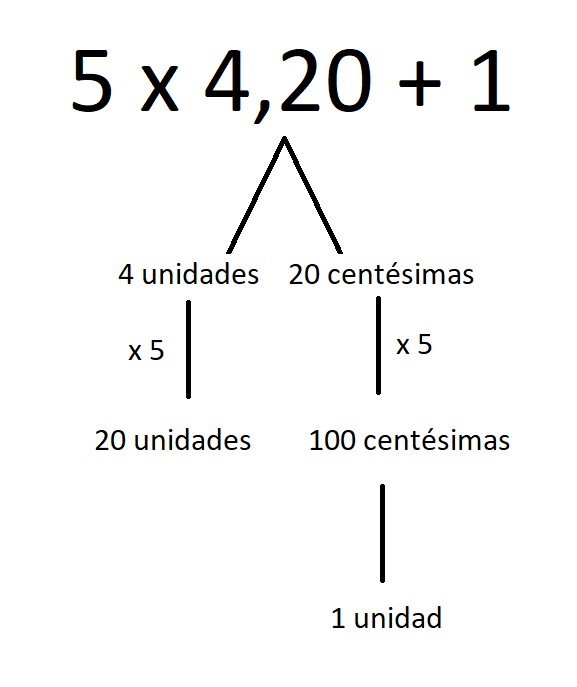
Cinco por cuatro veinte más uno veintidós
En muchas ocasiones se producen errores en la multiplicación de decimales por el mero hecho de no llamar a las cosas por su nombre. Comentábamos en el artículo anterior que es frecuente que los niños digan que 0,3 x 4 es 0,12 y que esto ocurre por no llamar a las cosas por su nombre, si dijéramos 3 décimas por 4 son 12 décimas, llegaríamos rápidamente a la conclusión de que 12 décimas es 1 unidad y 2 décimas y se escribe así: 1,2.
En el título de esta sección podría pasar algo parecido en caso de no dominar el número por dentro. ¿Qué juego de palabras se esconde detrás de esto?
¡Claro! Es que con «cuatro veinte» se refieren a 4,20. Es decir, a 4 unidades y 20 centésimas. Ahora bien, si al resolver la operación 5 x 4,20 + 1 no tenemos en cuenta que 100 centésimas son una unidad podemos encontrar niños (más de uno y más de dos) que digan que 5 x 4,20 es 20,100 y, al sumarle 1, pues no obtengan el «veintidós». Así que, si el niño ha ido construyendo poco a poco, no debería tener dificultad en decir que 5 x 4,20 son 20 unidades y 100 centésimas, o lo que es lo mismo, 21 unidades y al sumarle la otra unidad, obtengo 22.
Distinto es que la dificultad venga por la jerarquía de las operaciones… ¿Cómo trabajar la jerarquía? ¿Qué hacer para que comprendan por qué primero van los paréntesis, luego las multis y divis y luego lo demás?
¡¡¡Espera!!! ¿He dicho «comprendan»? ¡Pues claro! Es que la jerarquía se tiene que construir para comprender. No se trata de aprenderse el orden en que se hacen las cosas. Se trata de saber por qué se hacen y, si sabemos por qué se hacen sabremos en qué orden resolver.
***Nota mental*** Valorar la posibilidad de que la próxima entrada sea sobre la jerarquía de las operaciones ***Fin de nota mental***
Divisiones con decimales
Normalmente separamos las divisiones en tipos, en casos.
- Dividendo natural entre divisor natural (y saco decimales)
- Dividendo natural entre divisor natural (con dividendo menor que divisor)
- Dividendo decimal mayor que divisor entre divisor natural
- Dividendo decimal menor que divisor entre divisor natural
- Dividendo decimal entre divisor decimal
Bueno, o algo parecido a eso… La cosa es que en realidad no hay que actuar de manera diferente. ¡Dividir es dividir! Si dominamos el número por dentro y llamamos a las cosas por su nombre pues da igual «el tipo» o «el caso».
Algunos ejemplos:
Dividendo menor que divisor
Comentar en cada caso qué es lo que se está repartiendo es importante. Es importante llamar a las cosas por su nombre para que al hacer la prueba no olvidemos que el resto a sumar es 1 centésima (0,01) y no una unidad (1).
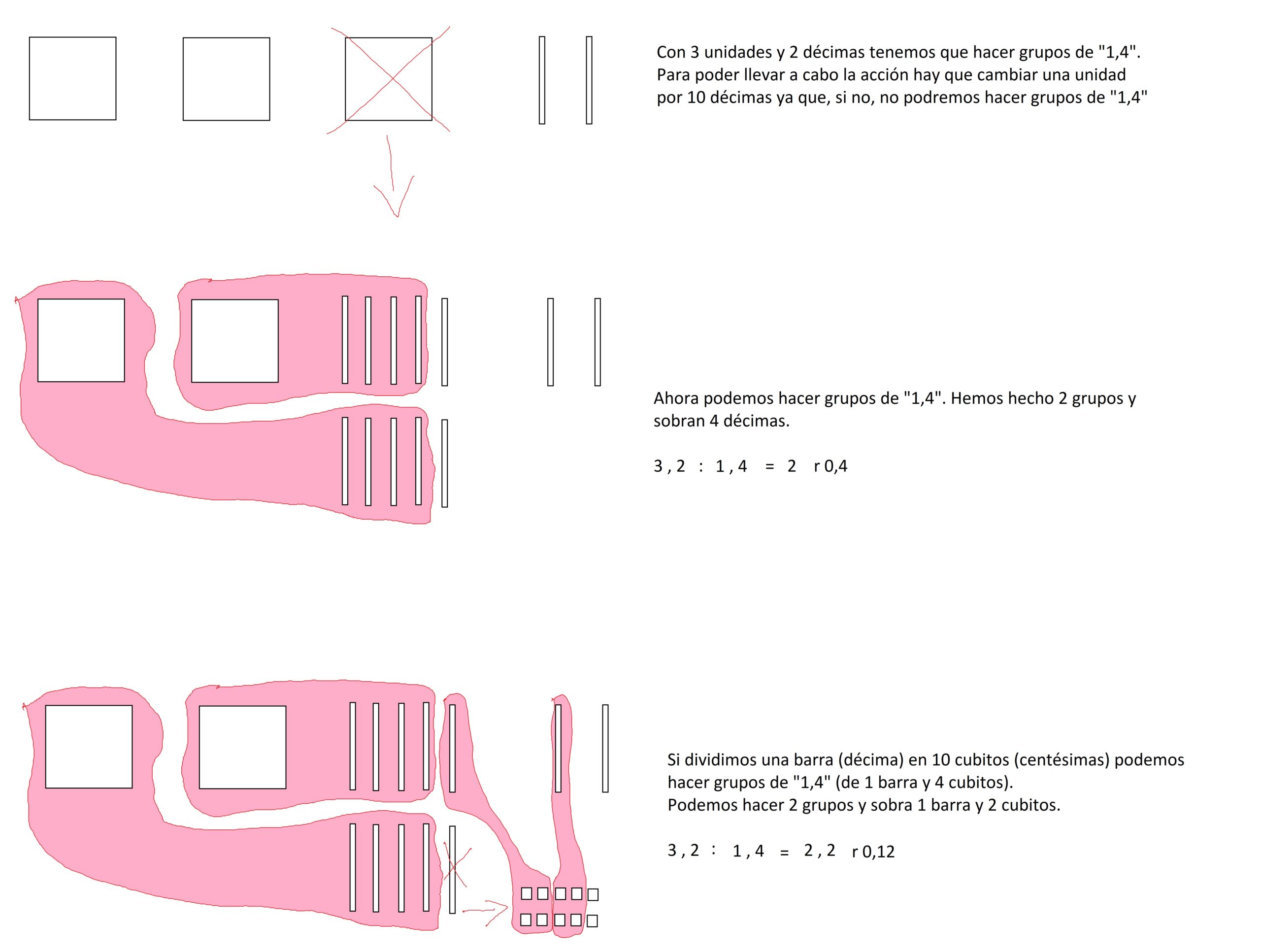
Vamos ahora con el caso más temido, el de los decimales en dividendo y divisor.
Decimales en dividendo y divisor
Luego podrás elegir el método que te apetezca de los vistos en este artículo.
¿Y es posible resolver de manera manipulativa divisiones con decimales en dividendo y divisor? Sí. Queda algo así. Para niños que están muy habituados a manipular es un buen método antes de dar el paso a lo simbólico y a la propiedad fundamental de la división (que es lo que se ha hecho en el caso de arriba).
3,2 : 1,4
Un poquito de porcentajes
Dije que en esta entrada tocaríamos también porcentajes desde lo hemos estado llamando «el número por dentro». Podría ser una entrada en sí misma. De momento, un adelanto (sin mucho detalle) para que veáis de qué hablo y como aplica todo lo anterior (las cosas por su nombre, las fracciones decimales…) al cálculo de porcentajes.
Por ejemplo: Queremos calcular, desde la descomposición, el 12% de 450. Podríamos hacer algo así:
Podemos descomponer 12 en 10 y 1 y 1. De ese modo facilitamos los cálculos.
10% de 450 es 45. Si sé el 10% de 450, automáticamente sé el 1% de 450 que es 4,5. Así que la operación se ha transformado en 45 + 4,5 + 4,5 = 54.
¿Otro ejemplo?
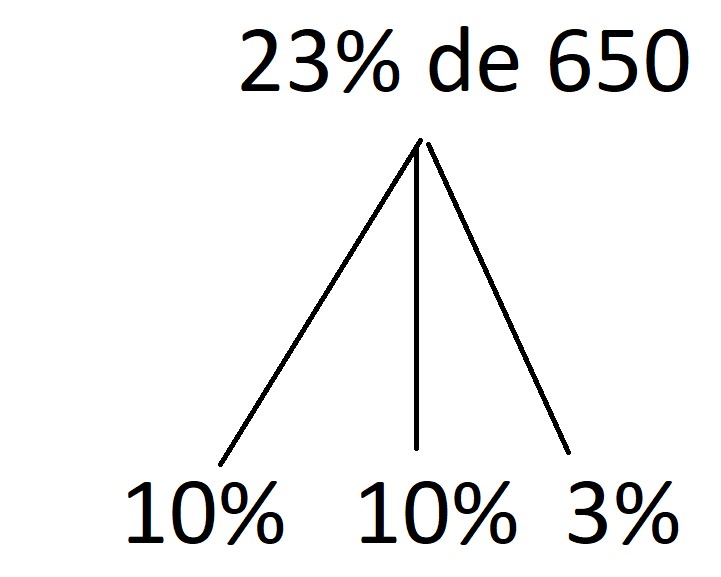
El 10% de 650 es sencillo, 65. Pero, ¿y el 3% de 65? Si sabes el 10% sabes el 1% y si sabes el 1% sabes el 3%.
El 1% de 650 es 6,5 así que el 3% de 650 es 6,5 x 3 o lo que es lo mismo 18 unidades y 15 décimas que es 19,5
Así que el 23% de 650 es 65 + 65 + 19,5 = 149,5
En conclusión
Si consigues que tu niño domine el UNO, lo que tiene dentro, lo que supone recibir el honor de ser llamado «UNO» ,entonces seguro que no tendrá dificultades en cálculo y me atrevo a decir que no tendrá dificultades, en general, en matemáticas. Y entonces, si domina el «uno» tu atención podrá dirigirse a la resolución de problemas, a la toma de decisiones, a la búsqueda de la estrategia, …
Y yo me vuelvo a preguntar: ¿Por qué esa obsesión en los últimos años con que los niños salgan de infantil haciendo cálculos «de alto nivel»? Por muy abiertos que sean los algoritmos, no deja de ser cálculo. ¿Y sabéis qué? Que existen las calculadoras. Que las calculadoras ya se encargan de hacer el trabajo «sucio».
¡Claro que tienen que saber calcular! ¡Claro que tienen que dominar los números! Eso es fácil, un poco tedioso (a veces) pero fácil. Al final todos sabemos calcular y, si no, tiramos de calculadora pero…
¿Puedes garantizar que tu alumno es capaz de trazar un plan? ¿De tomar decisiones? ¿De analizar todos los factores? ¿De predecir la solución sin hacer un solo cálculo? ¿De volver atrás y arrancar de nuevo? ¿Puede tu alumno resolver problemas o al menos enfrentarse a ellos?
Los problemas no son «cosa de las matemáticas». Los problemas, enfrentarse a ellos y buscar caminos para encontrar la solución son «cosa de la vida».
Lo importante no es contar sino lo que realmente cuenta (Bob Talbert).
Para leer el articulo original pincha aquí
Profe Bernabeu